
La matriz de confusión es una herramienta muy útil para valorar cómo de bueno es un modelo clasificación basado en aprendizaje automático. En particular, sirve para mostrar de forma explícita cuándo una clase es confundida con otra, lo cual nos, permite trabajar de forma separada con distintos tipos de error. En un post anterior de nuestro blog, explicamos detalladamente el concepto de matriz de confusión y sus métricas asociadas. Hoy planteamos un sencillo ejemplo de apliación.
Recordando nuestro «experimento» de predicción de infidelidad
Rescatamos para este post uno de nuestros experimentos anteriores. En concreto el de hicimos para explicar el algoritmo de regresión logística.
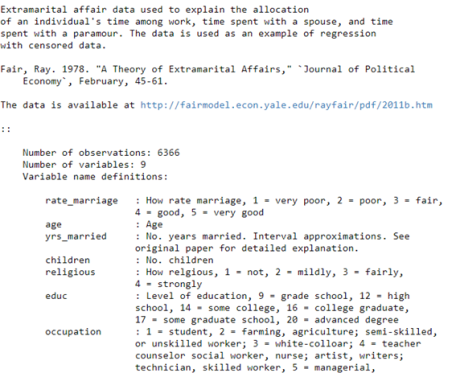
Si recordamos, trabajamos con el dataset “affairs”, basado en en una encuesta realizada por la revista Redbook en 1974, en la que se preguntaba a mujeres casadas por sus aventuras extramaritales. Este dataset, que cargamos desde la librería Staatsmodel, constaba de 6366 observaciones con 9 variables, de tipo «valoración de su matrimonio», «años de casada», «número de hijos», «nivel de estudios» etc.
Objetivo del modelo
El objetivo era crear un modelo que predijera si un individuo (en este caso, mujer) iba a ser “fiel” o “infiel”, basándose en el valor de esas 9 variables para el nuevo caso y en lo “aprendido” por el modelo a partir de los datos de entrenamiento (los datos de la encuesta).
Regresión logística
En este ejemplo, aplicamos el modelo de regresión logística de scikit-learn. Se trata de un modelo de probabilidad lineal, en el que la probabilidad condicionada es función lineal de los valores de las variables de entrada. Por tanto, obtenemos la probabilidad de que la variable dependiente tenga un valor categórico u otro (en nuestro ejemplo o “infidelity”= 0, o “infidelity”= 1), en función de los valores de las variables de entrada.
Evaluación del modelo
Llegado el momento de evaluar el modelo, es cuando vamos a echar mano de la matriz de confusión. Para ello, dividimos el dataset en dos partes. Dejamos un 75% de los datos como datos de entrenamiento (train), y reservamos el 25% restando como datos de prueba (test). A continuación, entrenamos el modelo de nuevo, pero ahora sólo con los datos de entrenamiento.
En el siguiente paso, lo aplicamos a los datos reservados como “test”, y ya evaluamos su rendimiento, calculando la matriz de confusión y las métricas exactitud (Accurary) y precisión (Precision).
Para mayor claridad, visualizamos la matriz de confusión en forma de mapa de calor.
Matriz de confusión
Merece la pena pararnos un momento a recordar el significado de la matriz de confusión y sus métricas asociadas, antes de pasar a interpretarla en nuestro ejemplo.

Los valores de la diagonal principal a=993 y d=176 se corresponden con los valores estimados de forma correcta por el modelo, tanto los verdaderos positivos_ TP(d), como los verdaderos negativos_TN (a).
La otra diagonal, por tanto, representa los casos en los que el modelo «se ha equivocado (c=316 falsos negativos_FN, b=107 falsos positivos_FP).
Exactitud
Si recordamos, la exactitud (o «accuracy«) representa el porcentaje de predicciones correctas frente al total. Por tanto, es el cociente entre los casos bien clasificados por el modelo (verdaderos positivos y verdaderos negativos, es decir, los valores en la diagonal de la matriz de confusión), y la suma de todos los casos.
Sin embargo, cuando un conjunto de datos es poco equilibrado, no es una métrica útil. Por ejemplo, si lo que intentamos predecir es una enfermedad rara, y nuestro algoritmo clasifica a todos los individuos como sanos, podría ser muy preciso (incluso un 99%), pero también, totalmente inútil.
Por ello, en estos casos se suele recurrir a otras métricas, como la sensibilidad (o recall), que representa la habilidad del modelo de detectar los casos relevantes, y que veremos un poco más adelante.
(El valor obtenido para este modelo es de un 73%. No es maravilloso, pero podemos considerarlo aceptable). Para calcularlo a mano, a partir de la matriz de confusión:
(993+176)/(993+176+107+316)=1169/1592= 0,73—73%
Precisión
La precisión, (o“precision”) se refiere a lo cerca que está el resultado de una predicción del valor verdadero. Por tanto, es el cociente entre los casos positivos bien clasificados por el modelo y el total de predicciones positivas. Para calcularlo a mano, a partir de la matriz de confusión:
(176)/(176+107)= 0,62— 62%
El valor obtenido para este modelo es de un 62%. Por tanto, nuestro modelo es más preciso que exacto.
Sigamos con otras métricas.
Sensibilidad, exhaustividad
La sensibilidad (o recall) representa la tasa de verdaderos positivos (True Positive Rate) ó TP. Es la proporción entre los casos positivos bien clasificados por el modelo, respecto al total de positivos. Para calcularlo en este caso:
176/(316+176)=0,35— 35%
Representa, como hemos dicho antes, la habilidad del modelo de detectar los casos relevantes. Un 35% es claramente un valor muy malo para una métrica. Podemos decir que nuestro algoritmo de clasificación es poco sensible, «se le escapan» muchos positivos.
Especifidad
La especificidad, por su parte, es la tasa de verdaderos negativos, (“true negative rate”)o TN. Es la proporción entre los casos negativos bien clasificados por el modelo, respecto al total de negativos. Para calcularlo a mano, a partir de la matriz de confusión:
993/(993+107)=0,90 —90%
En este caso, la especificad tiene un valor muy bueno. Esto significa que su capacidad de discriminar los casos negativos es muy buena. O lo que es lo mismo, es difícil obtener falsos positivos.
¿Qué métrica elegir?
La conveniencia de usar una métrica otra como medida del estimador dependerá de cada caso en particular y, en concreto, del “coste” asociado a cada error de clasificación del algoritmo.
En este ejemplo, la sensibilidad=0,35 y la especifidad=0,90. Por tanto, este modelo mucho más específico que sensible. Esta es la situación que nos interesa cuando nuestro objetivo es evitar a toda costa los falsos positivos.
Un ejemplo típico sería una prueba de dopping en un deportista. Si un falso positivo significa expulsarle de la competición injustamente, debemos evitar esta situación. En nuestro ejemplo sobre infidelidad, podemos decir que nuestro modelo evitaría «acusaciones injustas» 😉
Si lo que nos interesa es identificar los verdaderos negativos, (evitar falsos positivos) debemos elegir especifidad alta.
Por el contrario, si las «falsas alarmas» no nos preocupan, y lo que queremos evitar son los falsos negativos, nos interesa una mayor sensibilidad o recall.
Por ejemplo, no nos importa un falso positivo en una prueba de diabetes, ya que, indudablemente, la prueba se repetirá. Sin embargo, no nos interesa que una persona diabética no diagnosticada, no acceda rápidamente al tratamiento adecuado debido a un falso negativo.
Si lo que nos interesa es evitar falsos negativos, debemos elegir sensibilidad alta.
Conclusión
Este pequeño experimento, evidentemente, no tiene mayor utilidad que la de ayudarnos a aprender cómo funciona el algoritmo de regresión logística o cómo interpretar la matriz de confusión.
Un modelo no vale nada, si los datos sobre los que se ha entrenado no tienen ni el volumen ni la calidad suficientes (como en este ejemplo). Sin embargo, como vemos, la mejor manera de aprender es…¡haciendo! Para ello, no te pierdas nuestra colección de tutoriales sobre IA y Big Data.
The post Cómo interpretar la matriz de confusión: ejemplo práctico appeared first on Think Big.